Special Relativity: Time dilation
By SAJEEWA PEMASINGHE
Special theory of relativity was put forward by the German physicist Albert Einstein in 1905. It proposed radically new ideas that reshaped the classical views of relativity previously put forward by Galileo Galilei and Isaac Newton.

In the mid-1880s a series of experiments carried out by the American physicists A.A. Michelson and E.W. Morley implied that the speed of light (c) is independent of the motion of source relative to the observer. That is, everyone observes light to move at c regardless of how they move relative to the source or one another. This result cannot be proved true if we assume that the Newton’s laws of motion are correct.
In 1905 Albert Einstein included the implied result of the Michelson-Morley experiment as one of the postulates in his Special Theory of Relativity (SR). The two postulates of the SR are given below.
“The laws of physics are the same and can be stated in their simplest form in all inertial frames of reference”
In inertial frames, a body at rest remains at rest and a body in motion moves at a constant speed in a straight line unless acted on by an outside force.
“The speed of light c is constant, independent of the relative motion of the source and the observer”
Although they seem very innocent, these two postulates effect profound conceptual changes in the Newtonian perspective of motion. These include the loss of agreement on the elapsed time for an event, the variation of distance with speed, and the realization that matter and energy can be converted into one another.
In this article we are going to look at the effect of SR on the measurement of elapsed time for an event . This effect is specifically known as time dilation and it has to do with measurements of elapsed time by observers moving relative to one another.
Consider an astronaut in a spaceship which is travelling at a velocity v to the right relative to the earth. Suppose, that the astronaut measures the time it takes for light to cross his ship, bounce off a mirror, and return, as shown in Figure (a) below.
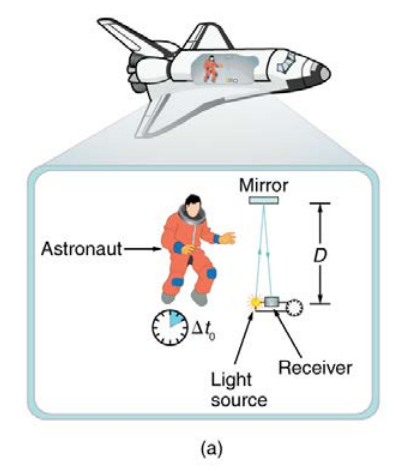
The astronaut is at rest relative to the spaceship and therefore sees the light travel straight across and back for a total distance of 2D, which is twice the width of his ship. We define proper time to be the time \Delta { t }_{ 0 } measured by an observer at rest relative to the process. So in this case proper time is measured by the astronaut since he is travelling at the same velocity as the spaceship and therefore is at rest relative to the process. Since time, is distance divided by speed \Delta { t }_{ 0 }=\frac { 2D }{ c }\quad \quad \quad \quad \quad (1)
The same event is observed by an earth-bound observer as shown in Figure (b) below.
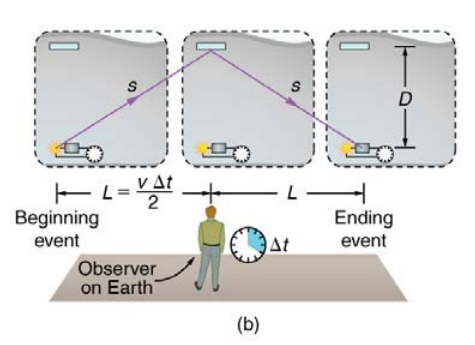
The earth-bound observer sees light taking a longer, triangular route as shown in Figure (b), thus travelling a distance of 2s . This ‘light taking a longer, triangular route’ might be a little difficult to imagine at first. You will be able to fully understand this observation of ‘light taking a longer, triangular route’ with respect to the earth’s frame of reference by watching the demonstration below presented by Professor Brian Cox.
Now, according to the second postulate, for both astronaut’s frame of reference and earth’s frame of reference light travels at the same speed, c. Therefore, since time is distance divided by speed, the time measured by the earth-bound observer is \Delta { t }=\frac { 2s }{ c } \quad \quad \quad \quad \quad (2)According to the earth-bound observer, by the time light bounces off the mirror and comes back, the spaceship has moved a distance 2L. Since distance is velocity multiplied by time,2L=v\Delta t\quad \quad \quad \quad \quad (3) The geometrical relationship between D, s, and L is shown below using the right triangle in Figure (c).
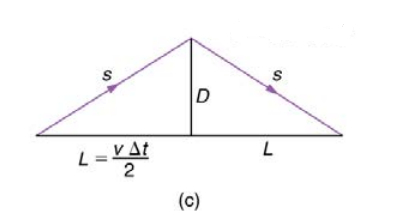
According to Pythagoras’ theorem, s=\sqrt { { D }^{ 2 }+{ L }^{ 2 } } \quad \quad \quad \quad \quad (4)Substituting for L in equation (4) using the relationship in equation (3) we get, s=\sqrt { { D }^{ 2 }+{ { \left( \frac { v\Delta t }{ 2 } \right) }^{ 2 } } } \quad \quad \quad \quad \quad (5)Substituting for s in equation (2) using the relation in equation (5) we get, \Delta t=\frac { 2 }{ c } \sqrt { { D }^{ 2 }+{ \frac { { v }^{ 2 }{ \left( \Delta t \right) }^{ 2 } }{ 4 } } } \quad \quad \quad \quad (6)Squaring both sides in equation (6) we get, { \left( \Delta t \right) }^{ 2 }=\frac { 4 }{ { c }^{ 2 } } \left( { D }^{ 2 }+\frac { { v }^{ 2 }{ \left( \Delta t \right) }^{ 2 } }{ 4 } \right) \qquad (7)Removing parenthesis we get, { \left( \Delta t \right) }^{ 2 }=\frac { 4{ D }^{ 2 } }{ { c }^{ 2 } } +\frac { { v }^{ 2 }{ \left( \Delta t \right) }^{ 2 } }{ { c }^{ 2 } } \qquad \qquad (8)Substituting for \frac { 4{ D }^{ 2 } }{ { c }^{ 2 } } using the relation in equation (1) we get, { \left( \Delta t \right) }^{ 2 }={ \left( { \Delta t }_{ 0 } \right) }^{ 2 }+\frac { { v }^{ 2 }{ \left( \Delta t \right) }^{ 2 } }{ { c }^{ 2 } } \qquad (9)Rearranging the terms we get, { \left( \Delta t \right) }^{ 2 }-\frac { { v }^{ 2 }{ \left( \Delta t \right) }^{ 2 } }{ { c }^{ 2 } } ={ \left( { \Delta t }_{ 0 } \right) }^{ 2 }\qquad (10)Taking the common factor outside, { \left( \Delta t \right) }^{ 2 }\left( 1-\frac { { v }^{ 2 } }{ { c }^{ 2 } } \right) ={ \left( { \Delta t }_{ 0 } \right) }^{ 2 }\qquad (11)Rearranging the terms we get, { \left( \Delta t \right) }^{ 2 }=\frac { { \left( \Delta { t }_{ 0 } \right) }^{ 2 } }{ 1-\frac { { v }^{ 2 } }{ { c }^{ 2 } } } \qquad \qquad (12)Taking the square root of both sides we get, { \left( \Delta t \right) }=\frac { { \left( \Delta { t }_{ 0 } \right) } }{ \sqrt { 1-\frac { { v }^{ 2 } }{ { c }^{ 2 } } } } \qquad \qquad (13)
According to equation (13), for any velocity v<c, \Delta { t }>\Delta { t }_{ 0 }Thus the earth-bound observer sees time-dilate (get-longer) for a system moving relative to the earth. Alternatively, according to the earth-bound observer, time slows in the moving frame, since less time passes there.
Note that if the relative velocity is much less than the speed of light \left( v\ll c \right) , then { { v }^{ 2 } }/{ { c }^{ 2 } } is extremely small, and the elapsed times \Delta t and \Delta { t }_{ 0 } are virtually equal. At low velocities, modern relativity approaches classical physics — our everyday experiences have very small relativistic effects.