One-way ANOVA manual and Pythonic

One-way ANOVA

Manual and Pythonic

By Sajeewa Pemasinghe

This method is used to find if there is a significant difference between the means of three or more groups at a given confidence level.

As the name ‘ANOVA’ suggests, this method analyses the variance in order to come to a conclusion. What type of variance? There are two types of variances:

  1. Between group variance
  2. Within group variance

So after finding these variances what does the method do? The following equation shows what the method does with the above two variances to come up with a statistic known as the F statistic.

F=\frac { Between\quad Group\quad Variance }{ Within\quad Group\quad Variance }\quad \quad \quad \quad \quad\quad\quad(1)

F=\frac { \left( \frac { Sum\quad of\quad Squares\quad Groups\quad (SSG) }{ degree\quad of\quad freedom\quad groups\quad ({ df }_{ groups }) } \right) }{ \left( \frac { Sum\quad of\quad Squares\quad Error\quad (SSE) }{ degrees\quad of\quad freedom\quad error\quad ({ df }_{ error }) } \right) }\quad \quad \quad \quad (2)

Let’s try to understand the calculation via an example.

30 students at a university were selected for an informal study about student study skills; 10 first year (Group A), 10 second year (Group B), 10 third year (Group C) undergraduates were randomly selected.

The students were given a study skills assessment. As researchers, we are interested in whether or not a difference exists somewhere between the three different year levels. We will conduct this analysis using the One-way ANOVA technique.

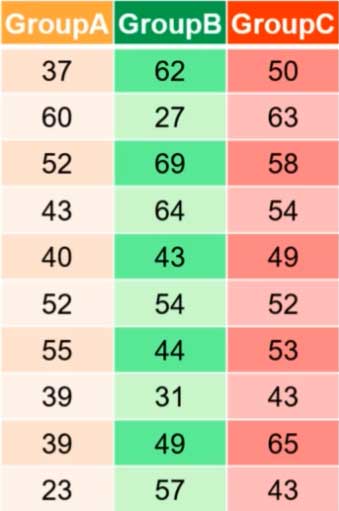
Calculation of ‘between group variance’
  1. Sum up the 30 scores and divide by 30 to find the overall mean ={ \mu  }_{ TOT}=49

  2. Calculate SSG
    • Find the difference between each group mean and the overall mean
    • Square the deviations
    • Add them up
    • Multiply by the number of items in each group
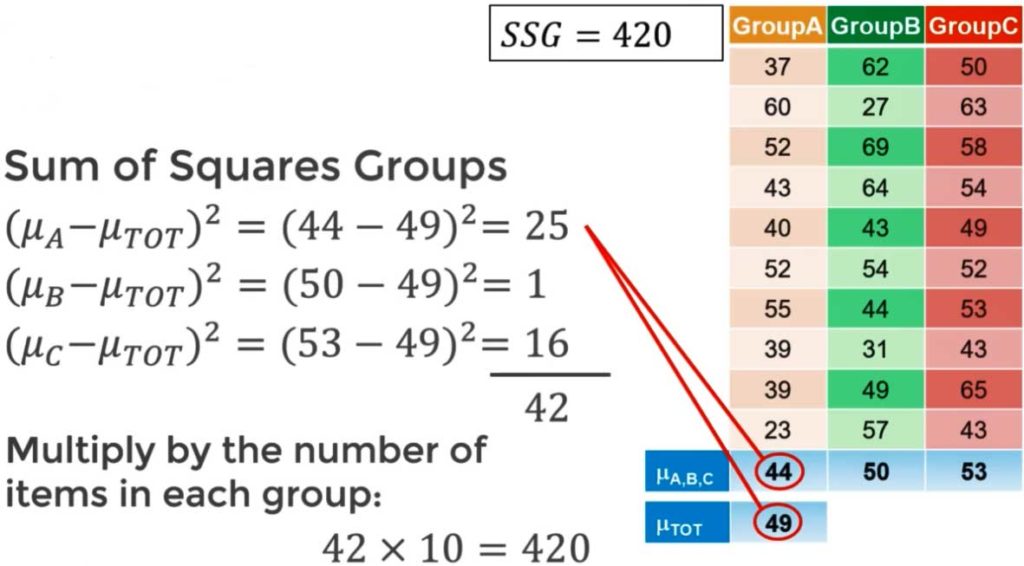
  1. Calculate { df }_{ groups }

    { df }_{ groups }\quad =\quad Number\quad of\quad groups\quad -\quad 1
    { df }_{ groups }\quad =\quad 3\quad -\quad 1\quad =\quad 2

  2. Finally calculate the ‘between group variance’between\quad group\quad variance\quad =\quad \frac { SSG }{ { df }_{ groups } }
    between\quad group\quad variance\quad =\quad \frac { 420 }{ 2 }
Calculation of ‘within group variance’
  1. Find the difference between each data point and its group mean
  2. Square each deviation
  3. Add up all the squared deviations to get SSE (30 squared deviations in this case)
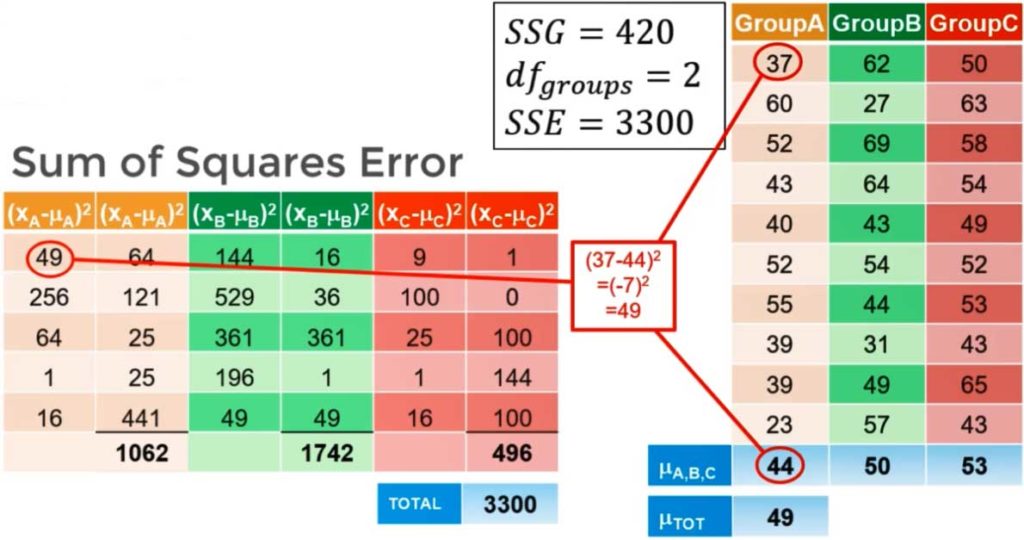
  1. Calculate { df }_{ error }

    \small{{ df }_{ error }\quad =\quad Number\quad of\quad data\quad points\quad -\quad Number\quad of\quad groups}
    \small{{ df }_{ error }\quad =\quad 30\quad -\quad 3\quad =\quad 27}

  2. Finally calculate ‘within group variance’

    within\quad group\quad variance\quad =\quad \frac { SSE }{ { df }_{ error } } within\quad group\quad variance\quad =\quad \frac { 3300 }{ 27 }  

Calculate the F statistic using equation (2) 

F=\frac { \left( \frac { SSG }{ { df }_{ groups } }  \right)  }{ \left( \frac { SSE }{ { df }_{ error } }  \right)  } =\frac { \left( \frac { 420 }{ 2 }  \right)  }{ \left( \frac { 3300 }{ 27 }  \right)  } =\frac { 210 }{ 122.22 } =1.718

 

F table lookup for numerator (groups) degrees of freedom = 2 and denominator (error) degrees of freedom = 27, at alpha = 0.05

 

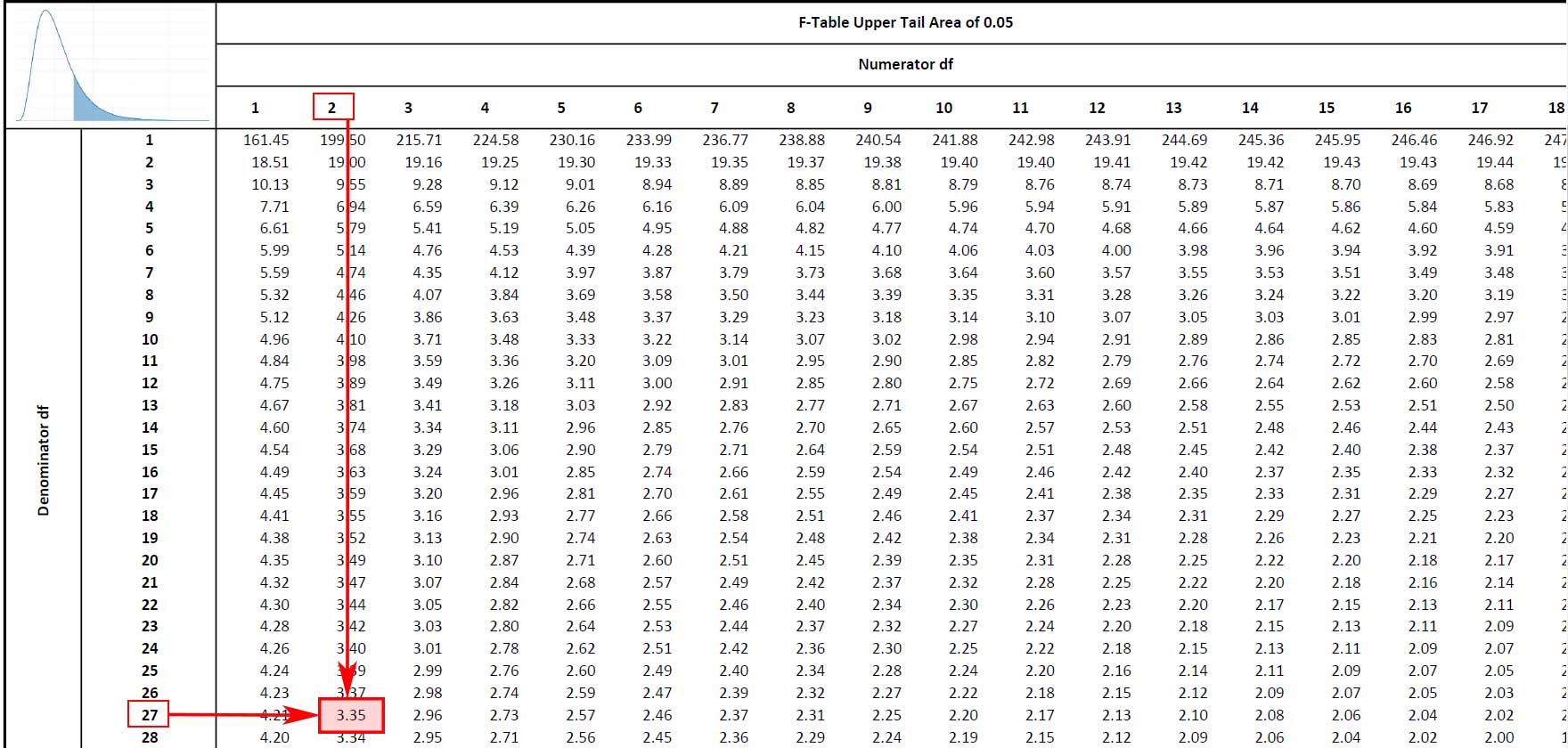
Conclusion

Our null hypothesis:  { H }_{ 0 }:\quad { \mu  }_{ A }\quad =\quad { \mu  }_{ B }\quad =\quad { \mu  }_{ C }

But F is less than { F }_{ critical }:\quad1.718<3.35

Therefore we fail to reject the null hypothesis!

Using Python programming language

from scipy.stats import f_oneway

groupA = [37, 60, 52, 43, 40, 52, 55, 39, 39, 23]

groupB = [62, 27, 69, 64, 43, 54, 44, 31, 49, 57]

groupC = [50, 63, 58, 54, 49, 52, 53, 43, 65, 43]

F_value,p_value=f_oneway(groupA, groupB, groupC)

print(F_value,p_value)

In our case the F_value variable gives 1.718 and the p_value variable gives 0.198. This 0.198 means that “The probablity of getting this F_value by chance is 0.198”.

Since 0.198 > 0.05 we can safely say that getting this F_value is not statistically significant at p=0.05. So we are unable to reject the null hypothesis!

Leave a Reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.